The 2017 Solar Eclipse Has a 'Relative' That Was Born in Japan in 1963

Last month, I reminisced about seeing my first total solar eclipse in July 1972. But my interest in solar eclipses actually began nine years before that, with a partial eclipse of the sun that I viewed from the Bronx on a rather cloudy, muggy Saturday: July 20, 1963. Toward the end of last month's story, I mentioned that the 1963 eclipse had a direct connection to our upcoming Great American Solar Eclipse. 

So now, allow me to explain.

It is an interesting phenomenon that an eclipse, whether of the sun or the moon, will repeat itself or return in a later year. Yet, to most people in today's society, the entire situation regarding eclipse times is seemingly a haphazard pattern. [Total Solar Eclipse 2017: Here Are the Best Live-Video Streams to Watch]

Not so, however, to those who lived more than two millennia ago.

Astronomers in Assyria and Babylonia kept track of time by carefully observing the motions of the sun and moon. By recording the details of solar and lunar eclipses, they markedly increased the accuracy of their measurements. And as they studied the record of centuries of eclipses, a pattern began to emerge: Eclipses tend to repeat themselves at intervals of just over 18 years, though they recurred at different localities on Earth. Such an interval is known as a saros. Actually, the length of a saros amounts to about 6,585 days — and it is composed of three different, and independent, lunar cycles that amazingly will periodically line up to create an eclipse. 

The first of these is the phase of the moon, which for a solar eclipse must be new. The mean interval between new moons, called a synodic month, is 29.5306 days. If we multiply this number by 223, we get 6,585.32 days.

Then, we need to get the moon to pass in front of the sun. This happens when a new moon occurs at or near a node, where the paths of the sun and moon appear to cross. The nodes skew westward around the ecliptic over a time frame of 18.6 years. Because of this, the sun will encounter the same lunar node every 346.6201 days, on average — a period that is known as the "draconic," or eclipse, year. Nineteen of these years works out to be 6,585.78 days.

Last, but not least, the moon's distance from Earth must also repeat to re-create the same type of eclipse. If the moon is closer to Earth than average, we'll end up with a total eclipse, but if the moon is farther away from Earth than average, its shadow will be too small to cover the sun completely, resulting in a ring, or annular, eclipse. All this depends on the "anomalistic month," which is the mean interval between lunar perigees (when the moon is closest to Earth) or apogees (when the moon is farthest away). The mean time scale here amounts to 27.55455 days. Multiplying this value by 239 gives us 6,585.54 days.

So all three cycles almost exactly coincide in 18 years and 15 1/3 days, minus the number of leap years that intervene between eclipses. In most cases, this is equal to either 18 years, 10 1/3 days, or 18 years, 11 1/3 days, since five or four leap years, respectively, almost always occur in this cycle with nearly equal frequency. As such, the circumstances of a particular eclipse will very nearly repeat after this 18.03-year interval.

The saga of saros 145

The most changeable factor can be traced to that one-third of a day fraction. During that 8-hour interval, our planet rotates one-third of the way around on its axis, causing the paths of subsequent eclipses to occur about 120 degrees of longitude farther to the west. Thus, after three repetitions (54 years and 32 days, plus or minus one day) an eclipse will recur in the same general part of the world. This is sometimes referred to as a "triple saros," although the Greeks called such a period an "Exeligmos."

After three saroses, the longitude of the eclipse path is approximately the same as the first one, but it is now shifted about 600 miles to the north or south.  

Typically, a saros period lasts between 1,244 and 1,514 years. Eclipse paths migrate north or south from pole to pole, and the period begins and ends with partial eclipses. In the interim, as many as six- to seven-dozen member eclipses can occur. The upcoming eclipse belongs to saros 145, which began with an exceedingly slight partial eclipse over western Siberia on Jan. 4, 1639, and will continue until April 17, 3009, ending with a small partial eclipse over Antarctica and involving a total of 77 events. [Solar Eclipses Through the Ages: From (Possible) Beheadings to Science]

Relatives of the Great American Solar Eclipse

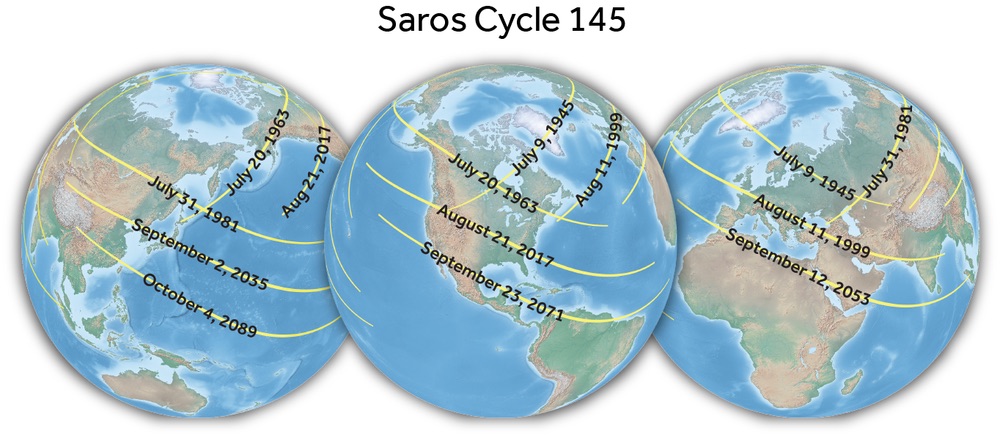
Now, as to the relationship between the 1963 eclipse of my childhood and the upcoming Great American Solar Eclipse, check out the graphic below, courtesy of Michael Zeiler's wonderful greatamericaneclipse.com/ website, depicting three globes representing the Earth and some of the eclipse paths belonging to members of saros 145. In particular, concentrate on the middle globe, where we see the paths of the July 20, 1963, eclipse and the upcoming Aug. 21, 2017, event. If you do a quick calculation, the 1963 and 2017 eclipses are separated by 54 years and 31 days — a triple saros/Exeligmos. So you can see that both eclipses are indeed "related." The 1963 eclipse cut a path starting at Japan's Hokkaido Island (check the left globe), then headed southeast across southern Alaska through Canada and also through Maine. 

Now look at the globe on the right. One saros (18 years, 11 1/3 days) prior to the 1963 eclipse, a total eclipse on July 9, 1945, swept across northern Europe. Go back to the middle globe for a moment, and you'll see that the westernmost extension of this path started over the northern Plains of the U.S. 

In 1963, that one-third of a day kicks in, and the path falls over North America, about 120 degrees to the west. One saros later, check the left globe and examine the path of the July 31, 1981, eclipse that streaked over Siberia. Another 18 years and 11 1/3 days go by, and if you check the right-hand globe again, we come to Aug. 11, 1999 — a total eclipse that crossed parts of Europe. 

So after three saroses, the 1963 eclipse has returned in 2017 to North America, except it has now shifted farther to the south, setting the stage for the first coast-to-coast totality for the contiguous U.S. in 99 years.

Ranking eclipse-observing expertise 

George Lovi (1939-1993), a longtime friend of mine, for many years wrote the Ramblings column in Sky & Telescope magazine. Whenever we were coming up on an impending total eclipse, George would rather cryptically ask prospective observers, "How many saroses have you completed?" George always considered seeing two consecutive members of a saros family something akin to a "black belt" accomplishment. 

I am hoping to complete my fourth saros on Monday from a special eclipse flight charted by Alaska Airlines that will fly about 1,000 miles west of the Oregon coast over the Pacific Ocean. I had seen the previous member of saros 145 from a ship off Nova Scotia on Aug. 11, 1999 (check the middle globe). 

Interestingly, I've seen two eclipses from saros 120, but they are not consecutive. I saw the Feb. 26, 1979, total eclipse from Roy, Montana, and the March 20, 2015, totality from an aircraft flying over the Faroe Islands near the Arctic Circle. However, I decided to pass on the March 9, 1997, eclipse — for some reason, I just couldn't get excited about trekking to Mongolia! And George never provided a criterion for seeing two nonconsecutive members of a particular saros. 

So maybe for saros 120 I should get a red belt instead of a black. 

Joe Rao serves as an instructor and guest lecturer at New York's Hayden Planetarium. He writes about astronomy for Natural History magazine, the Farmers' Almanac and other publications, and he is also an on-camera meteorologist for Fios1 News in Rye Brook, New York. Follow us @Spacedotcom, Facebook and Google+. Original article on Space.com.