How Lagrange points solved one of physics' biggest problems

Paul M. Sutter is an astrophysicist at The Ohio State University, host of "Ask a Spaceman" and "Space Radio," and author of "Your Place in the Universe" (Prometheus Books, 2018). Sutter contributed this article to Space.com's Expert Voices: Op-Ed & Insights.

There aren't a lot of guarantees in life, and there are even fewer in space. Everything is moving; everything is chaotic. "Life" in the solar system is in constant motion.

But there are certain special places. They're like islands of stability, spots of reprieve where a weary traveler can rest, take in the sights, get some science done. They are the Lagrange points, and they're important.

The three-body problem 

The origins of the Lagrange points are sunk deep within one of the most difficult problems faced by mathematicians and physicists over the past 400 years: the three-body problem.

Isaac Newton's law of universal gravitation is astoundingly simple to write down. It's just a single equation that can be used to predict things ranging from the flights of cannonballs to the orbital speed of the moon. In fact, any time you're trying to work out the gravitational interaction of two bodies, the math is super simple, easy to solve and easy to write down. Once you write down the solution, you can predict the behavior of those bodies as far into the future as you desire.

But once you introduce a third body, everything goes haywire. There is no easily notated solution that predicts how three objects will interact via their mutual gravity. In the modern age, only computers can crunch the raw numbers to deliver results. Our ancestors, however, were lost in mazes of unsolvable math.

Related: The 'three-body problem' has perplexed astronomers since Newton formulated it. A.I. just cracked it in under a second.

Some super-geniuses, though, found carefully constructed situations that allowed them to solve the three-body problem. One of them was Leonhard Euler, the Swiss polymath who wrote more papers than entire generations of other mathematicians. In 1722, he found some narrow solutions to the three-body problem when one of the objects has essentially no mass.

Following up on this 50 years later, Italian-French scientist Joseph Louis Lagrange extended Euler's work. And because Euler already has a multitude of things named after him, later scientists gave the full credit to Lagrange — hence the term "Lagrange points." 

Finding the point 

Euler and Lagrange made some simplifying assumptions. They looked at the problem of three objects interacting via gravity. But they looked only at the two-dimensional picture of the objects' orbits, ignoring other motion. They also assumed that one of the objects had such a small mass in relation to the other two that its own gravity could be ignored.

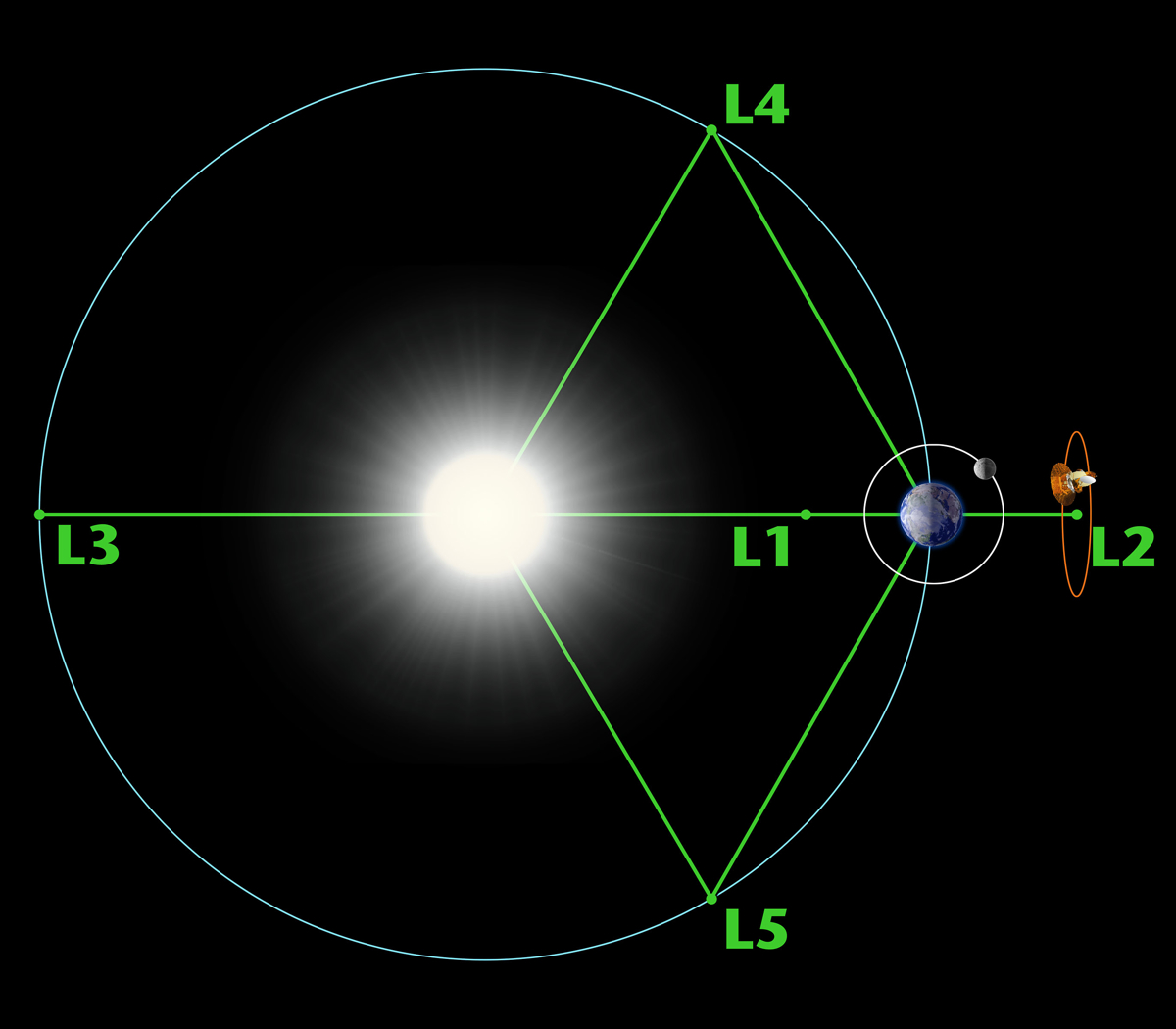
With those assumptions in place, they were able to write down a solution to the three-body problem. In that solution, they found five peculiar places where the forces acting on the third object canceled out. These are the Lagrange points. (Euler found the first three, and Lagrange discovered the next two.)

The first three points — commonly denoted as L1, L2 and L3 —​​ sit along a line connecting the two bigger masses. If we take the sun-Earth system as an example, L1 sits within Earth's orbit, L2 sits outside it and L3 is on the opposite side of the sun.

These three points are locations where the forces on a third object — a satellite, a speck of dust, whatever, as long as it's small — cancel out. Consider L1, which is about 930,000 miles (1.5 million kilometers) closer to the sun. Usually, an object closer to the sun will have a faster orbital speed, but at this precise position, Earth's gravity tugs on the object in just the right way so that L1 maintains the same relative position.

The opposite is true for L2. Usually, an object out there will have a slower orbit, but again, Earth's gravity tugs it forward, keeping it in sync. L4 and L5 sit behind and in front of Earth in its orbit, forming an equilateral triangle with the sun and Earth. There, the effect is the same, with the forces of the sun and Earth equally balancing each other out.

Interplanetary service stations 

Of the five Lagrange points, L1, L2 and L3 are unstable. You can put something there, and technically, everything balances. But the slightest nudge will send it away — just like putting a pencil on its tip is a balanced system, but not for long. In contrast, L4 and L5 are stable; objects there tend to stay for the long haul.

Every pair of massive objects in the solar system comes with its own set of Lagrange points. So there are five points for the sun-Earth pair, the Earth-moon system, the sun-Jupiter system and so on.

When it comes to Jupiter, its L4 and L5 points are so stable that they've collected their own set of asteroids, known as the Trojans. These asteroids have led and followed the gas giant in its orbit for millions of years.

Earth's L4 and L5 points have their own small collections of rocks, but when it comes to spaceflight, the L1 and L2 points are much more interesting. Even though they're unstable, they're not very unstable, so you don't have to work hard to keep a spacecraft near them.

L1 is a great place for observing the sun, since you can put your camera on one side of the spacecraft and your communications gear on the other, and you'll always be in a direct line between the sun and Earth. This is precisely where NASA and the European Space Agency placed the Solar and Heliospheric Observatory.

L2 is a great place for observing anything but the sun. Once again, the alignments of the orbits allow for uninterrupted communication with Earth, and the sun is always in the same position for providing solar power. The James Webb Space Telescope recently arrived at L2 to begin its science observations.

Learn more by listening to the "Ask A Spaceman" podcast, available on iTunes and askaspaceman.com. Ask your own question on Twitter using #AskASpaceman or by following Paul @PaulMattSutter and facebook.com/PaulMattSutter.