Kepler's Third Law: The movement of solar system planets
Before Johannes Kepler’s Third Law, the motions of the planets around the Sun were a mystery.

Breaking space news, the latest updates on rocket launches, skywatching events and more!
You are now subscribed
Your newsletter sign-up was successful
Want to add more newsletters?
Kepler’s Third Law is the last of the revolutionary theorems by German astronomers Johannes Kepler and explains planetary orbits around the sun.
Before Kepler outlined his laws of planetary motion in the early 17th century, humankind’s knowledge of the solar system and beyond was in its infancy and largely remained a mystery. At the time of Kepler the notion was that the Earth was the center of the solar system, and perhaps of the universe itself.
Even the more accurate heliocentric models of the solar system that placed the sun at their center were incomplete, suggesting that the planets move in neat circles around their stars.
Article continues belowRelated: Solar System Planets: Order of the 8 (or 9) Planets
Kepler’s laws would shift the star from the center of this model slightly to a focal point instead, flattening the orbits of planets, and suggest that these planetary bodies move at speeds that vary depending on proximity to their star.
Johannes Kepler
The first seeds of Kepler’s laws were planted before his 1571 birth in the Free Imperial City of Weil der Stadt, which is now part of the Stuttgart Region in the German state of Baden-Württemberg to father Heinrich Kepler and mother Katharina Guldenmann.
They predate his 1577 observation of The Great Comet, which fostered within the young man a fascination with astronomy that would last his entire life. Or his observation of a lunar eclipse in 1580 that cemented this preoccupation.
Breaking space news, the latest updates on rocket launches, skywatching events and more!
A more significant event for Kepler occurred in 1543, before his birth, when Nicolaus Copernicus published his theory that the Earth revolves around the sun in his book On the Revolutions of the Celestial Spheres.
The theory would spark a major scientific revolution — aptly named the Copernican revolution. Kepler and others would eventually ride this wave and build upon Copernicus’ work to overturn geocentric models that suggested that the sun and the other solar system bodies revolve around the Earth.

In August of 1600, Kepler was banished from Graz, Austria, freeing him up to travel across the Danube to Prague, to work for famous astronomer Tycho Brahe.
Brahe was considered at the time to be the author of the most accurate observations in astronomy, and he saw the potential of Kepler’s studies. This didn’t mean he entirely trusted his new assistant.
Kepler was exposed only to part of Brahe’s planetary data, lest he should eclipse his new mentor. This fear of Kepler’s potential may well have been Brahe’s motivation for setting him the task of better understanding the orbit of Mars. As Kepler worked on this problem, Brahe set about perfecting his own geocentric model of the solar system with Earth at its center.
Not only did the orbit of Mars not fit well with the geocentric model, but it was also a problem for early Copernican models that suggested the orbits of the planets were perfect circles.
Thus, Kepler came to the realization that the orbits of the planets were not circular, but were flattened circles or ellipses. By handing Kepler the study of the orbit of Mars — that most elliptical planetary orbit — Brahe had unwittingly unraveled his own geocentric model before its completion and had facilitated the creation of laws that would help cement heliocentrism as the accepted model of the solar system.
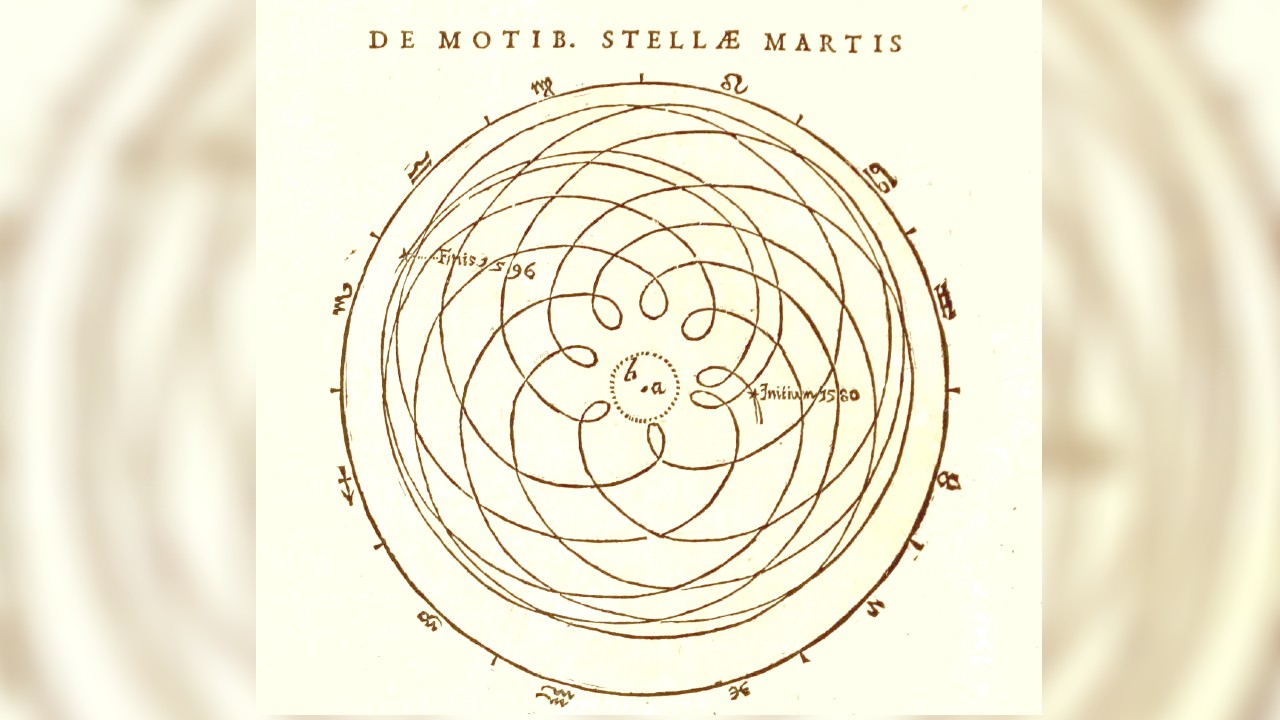
Properties of ellipses laws one and two
One of the keys to understanding Kepler’s laws of planetary motion lies in the properties of ellipses.
The first property of ellipses is that they are defined by two focus points — the foci. The sum of distances to any point on an ellipse is always a constant. For planetary orbits, this leads to Kepler’s first law, “the orbit of a planet is an ellipse with the Sun at one of the two foci.”
This means that the planet and its star orbit a mutual center of mass, but because the star’s mass is so much larger that its planet, that center of mass isn’t just closer to the star, it's often beneath its surface.
The second property of an ellipse defines the difference between this shape and a circle. An ellipse is a flattened circle, this “flatness” is defined as eccentricity and takes a value between 0 and 1. So a perfect circle can be thought of as an ellipse with an eccentricity of 0. A parabola would be an ellipse with an eccentricity of 1.
Related: What is astronomy? Definition & History
For Kepler’s second law, imagine a planet on an elliptical orbit with a line joining it to its parent star. As the planet moves the line sweeps out an area that is the same at all times.
Yet because of the eccentricity, when a planet is closer to its star the line between the two is shorter. This means the area it traces is shallower. Thus, to map out the same area in the same amount of time, the planet must move more quickly.
So, Kepler’s second law tells us that when a planet is closest to its star — a point called the perihelion — it moves at its quickest. On the flip side of this, when the planet is furthest from its star — at the aphelion — the planet moves at its slowest.
It’s natural to group these two laws together as they were born from Brahe’s closely guarded observations and were published together in the 1609 work Astronomia nova (New Astronomy).
Kepler’s third law, also known as The Law of Harmony, would take another ten years to formulate. Published in 1619, it would reveal the solar system’s mechanics in unprecedented detail.
A harmonic third law
“The square of the orbital period of a planet is proportional to the cube of the semi-major axis of its orbit.”
That’s Kepler’s Third Law in a nutshell, and it arises from the third physical property of ellipses, related to its various axis points. The longest axis of the ellipse is called the major axis, while the shortest axis is called the minor axis. Half of the major axis is termed a semi-major axis.
The equation for Kepler’s Third Law is P² = a³, so the period of a planet’s orbit (P) squared is equal to the size semi-major axis of the orbit (a) cubed when it is expressed in astronomical units.
What Kepler’s Third Law actually does, is compare the orbital period and radius of orbit of a planet to those of other planets. Thus, unlike Kepler’s first and second laws that describe the motion characteristics of a single planet, the astronomer’s third law compares the motion of different planets and calculates the harmonies of the planets.
This comparison takes the form of the ratio of the squares of the periods (T²) to the cubes of their average distances from the sun (R³), finding it to be the same for every one of the planets.
Thanks to this law, if we know a planet’s distance from its star, we can calculate the period of its orbit and vice versa. Because the distance between Earth and the sun (1 AU) is around 92,960,000 miles (149,600,000 kilometres) and one Earth year is 365 days, the distance and orbital period of other planets can be calculated when only one variable is known.
For the solar system, that gives us an accurate picture of every planet’s orbit around the sun.
As a planet’s distances from the sun increase, the time they take to orbit the sun increases rapidly.
For example, Mercury - the closest planet to the sun-completes an orbit every 88 days. The third planet from the sun, Earth, takes roughly 365 days to orbit the sun. And Saturn, the solar system’s sixth planet out from its star, takes 10,759. Of course, The Harmonic Law doesn’t just tell us about the orbits of planets.
Using Kepler’s Third Law
One thing that may be noticeable to you about Kepler’s Third Law is that it makes no mention of an object's mass. Yet, thanks to the application of Newton’s laws of gravity, physicists arrive at a more generalized form of the equation.
Related: What Is Quantum Gravity?
This generalized form of the third law equation can be used to find the masses of the bodies involved in the system described. Given mass 1 (m1) and mass 2 (m2), the masses of the two bodies, m1 describing the star is usually so significantly larger than m2 that the mass of the orbiting body can be ignored.
And with this in mind, the Harmonic Law has been successfully used to calculate the masses of planets in our solar system, with accurate masses and mean densities found for Mars, Jupiter, Saturn, Uranus, and Neptune.
This extends beyond planets and stars and can be applied to planets and their moons and even artificial satellites placed in orbit around them.
The recent placement of artificial satellites around Venus has enabled the mass and mean density of Venus to be accurately found. Additionally, the total mass of the Pluto-Charon system has been determined using the harmonic law.
Astronomers have successfully used the third law to obtain measurements of the highly elliptical orbits of comets around the sun.
But Kepler’s Third Law isn’t just useful in the solar system.
Kepler’s Third Law beyond the solar system
Astronomers have discovered over 4,000 planets beyond the solar system and thanks to Kepler’s laws, can calculate their orbits and their masses.
Because other stars have different masses to the sun, Kepler’s Third Law undergoes a slight adjustment to calculate the masses of their planets. For exoplanets, the formula is modified to account for the variation in the star’s mass as compared with our sun. So astronomers use R = (T² x Ms)¹/3 where Ms is the star’s mass in relation to our sun’s mass, to calculate the mass of an exoplanet.

Kepler’s Third Law in combination with his second law has enabled us to derive the masses of stars in binary systems, vital to understanding both the structure and evolution of stars.
To do this, astronomers use the binary mass function, which is derived from Kepler’s third law and the fact that bodies orbit a mutual center of gravity. When considering stars and planets, this is much closer than the star because of the planet’s much smaller mass. For Binary stars however, we can’t make the same assumptions and we can’t just disregard m2, because in these cases it's much closer to m1. Fortunately, for binary stars, if astronomers know the period of the stars (T) and their average separation (a) then they can still work out the sum of the masses of the two stars.
That means The Law of Harmonies is now used in planetary systems wildly different to our own. Systems that Kepler could have barely dreamt of, as he started out on the Great Comet in the 16th Century.
Johannes Kepler died on November 15, 1630.
Beyond his laws of planetary motion, his legacy lives on in the form of the Kepler space telescopes which have made vital contributions to the discovery of planets outside the solar system, and craters on both the moon and Mars among a host of other things.
Of course, no single astronomer or scientist can be credited with our understanding of the Universe. The biggest gap in Kepler’s laws was the fact that the early astronomer couldn't explain the force holding the planets to the relationship he observed.
Just as Kepler built of the work of Copernicus, Isaac Newton would eventually come along and use Kepler’s laws to derive his theory of gravity. And Albert Einstein would eventually build on this work to develop his theory of general relativity.
There is a very good chance that when Newton famously said “If I have seen further, it is by standing upon the shoulders of giants,” he had Kepler and his laws of planetary motion at the forefront of his mind.
Additional resources

Robert Lea is a science journalist in the U.K. whose articles have been published in Physics World, New Scientist, Astronomy Magazine, All About Space, Newsweek and ZME Science. He also writes about science communication for Elsevier and the European Journal of Physics. Rob holds a bachelor of science degree in physics and astronomy from the U.K.’s Open University. Follow him on Twitter @sciencef1rst.
