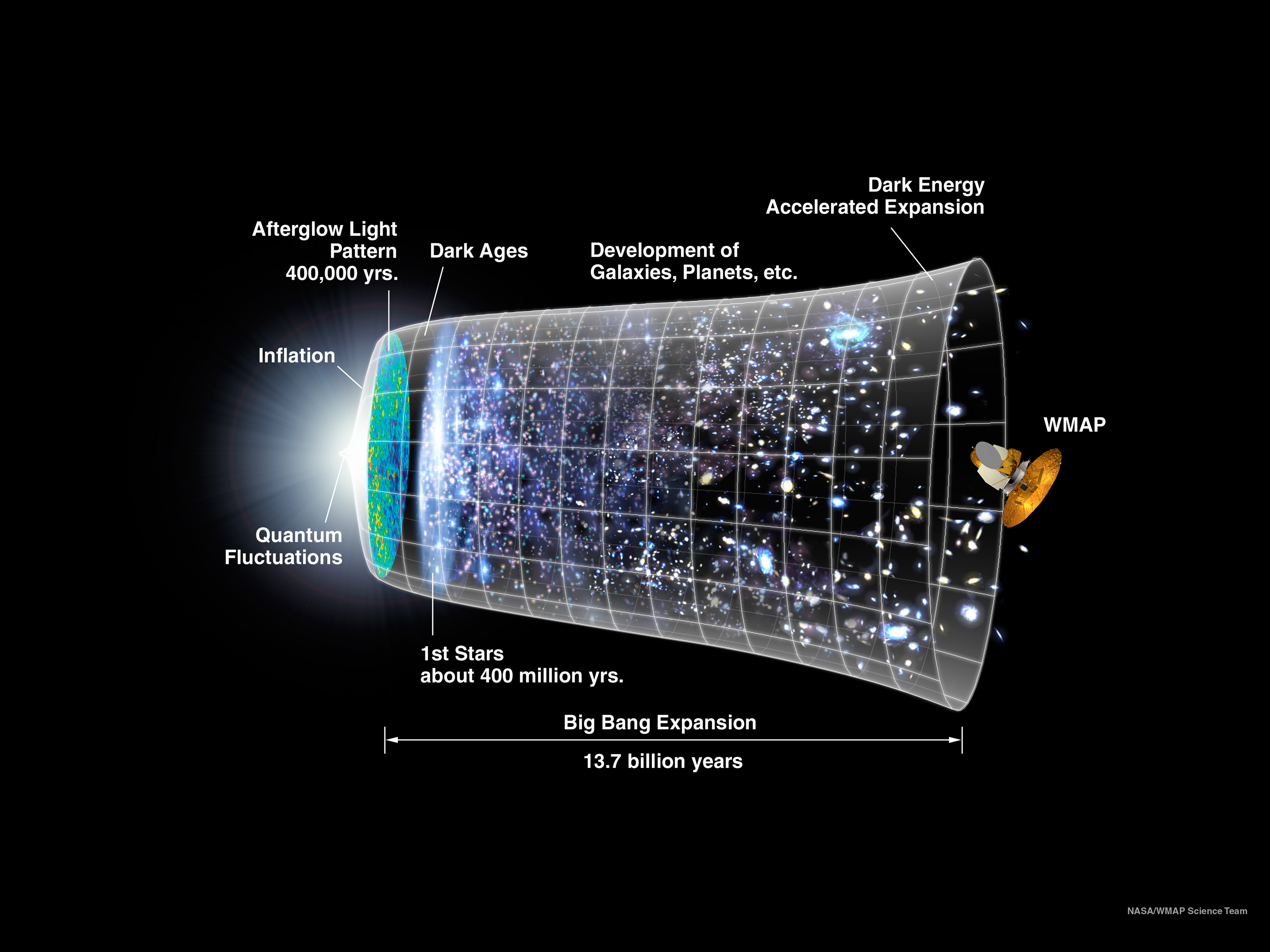
Is the Big Bang Cycling Through Hidden Time?

Edward Belbruno is a mathematician and an artist. His paintings are in major collections and exhibited throughout the United States, and he regularly consults with NASA from his position as a cosmology researcher at Princeton University. He is also author of "Fly Me to the Moon" (Princeton University Press, 2007). Belbruno contributed this article to Space.com's Expert Voices: Op-Ed & Insights.

Who hasn't looked up at the star-studded night sky and wondered, "Where did everything come from?" 

There are many ways to address this question. It was Edwin Hubble whose telescopic observations of galaxies in 1929 led to the major discovery that the universe is expanding, and that the rate of expansion is proportional to how far the galaxies are from one another. The farther apart they are, they faster they are going. This result implies there was a time about 13.75 billion years ago when the universe began in an event we now call the Big Bang. 

The Big Bang

The evidence suggests the Big Bang was something mind-blowing in its scale, described in the theory of inflation, first presented by Alan Guth in 1979 and elaborated upon in his book "The Inflationary Universe" (Perseus Books, 1997). Guth suggests the entire universe came essentially out of nowhere, at a rate that is incomprehensible: Within a trillionth of a trillionth of a trillionth of a second, the universe expanded by a factor of 10⁷⁸ in volume — that's a 10 with 78 zeros after it. We really have no idea how this happened, which naturally gives rise to many theories.

Cyclic universes

The cyclic universe theory is an attempt to try and understand how the Big Bang could have occurred. Put forth by Albert Einstein in 1931, the theory suggests that prior to the Big Bang, there was another universe that existed. This universe expanded, then contracted into what is called a "big crunch," and its contraction led to the Big Bang that created our universe. 

According to that theory, our universe could do the same thing. In fact, there could have been a whole sequence of such universes, expanding and contracting, perhaps going on forever. 

There are more recent variations of this idea. One of these is the interesting work by Paul Steinhardt of Princeton University and Neil Turok of the Perimeter Institute. They have a cyclic universe theory, called the ekpyrotic theory, where the Big Bang itself is modeled as the collision of higher dimensional objects called branes, derived from string theory, elaborated in their book "Endless Universe" (Doubleday, 2007). 

Another cyclic theory is called loop quantum cosmology, based on quantum gravity. In this theory the Big Bang is replaced by a quantum bounce. This is when a universe collapses and as it compresses down, the compression is limited by tiny loop structures in the fabric of space and time, called quantum loops. At the end of the compression, expansion begins and is influenced by the quantum effects within the quantum loops. This transition between compression and expansion is called a quantum bounce. 

How numbers link universe to universe

But how does one universe transition to another? For the last two years, I have been trying to answer that question from a rigorous mathematical perspective. I apply mathematical techniques from the field of regularization theory within the field of celestial mechanics, and try and see if a cyclic universe is even mathematically possible. 

This is done by showing that the equations defining the Big Bang can be rewritten so as to make sense at the moment of the Big Bang. This is necessary, since the equations defining the evolution of the universe after the Big Bang, called the Friedmann equations, break down at the Big Bang itself and make no sense. [Hidden Time in the Art of Ed Belbruno (Photos)]

Regularization theory provides a way for these equations to be rewritten in a new form so they can be defined at the Big Bang. If this is done correctly, then it also provides a way to understand if variation in the parameters defining the universe can be described at and near the Big Bang as time varies. We then say that the Big Bang has been "regularized." Once this is done, then it can be determined if it is mathematically possible for a transition from a big crunch to a Big Bang to occur. 

The way the way regularization works is as follows: The Friedmann equations describe the evolution of the universe from the Big Bang as time progresses. They are obtained using Einstein's general theory of relativity and yield values that describe the evolution of several different parameters as time varies. The variables include the Hubble variable, which describes rate of change of the scale of the universe, and the "equation of state," which is the ratio of the pressure and the density of the universe. 

There are several others, including the curvature of the universe, which measures the degree to which the universe bends space and time, and the anisotropy, which is a measure of how nonuniform the universe is in different directions. Although there are several parameters of interest, the key ones for my analysis are the Hubble variable and the equation of state. This is because I am concerned with how the universe behaves at and near the Big Bang. The Hubble variable is important since it is related to the scale, or size, of the universe and how that varies. The equation of state is important since it yields values it must have for regularization to be possible. These two variables give a pretty good picture of what is going on.

Understanding time near the Big Bang

If we use the symbol "t" for time, then let's assume the Big Bang occurs at t=0, so that relative to us, the Big Bang occurred t=13.75 billion years ago. The Friedmann equations are defined for t greater than 0, or t less than zero, but when t=0, these equations run into trouble. This is because the Hubble variable has the value of infinity at t=0. This follows since that variable is proportional to how fast the universe expands, which is infinite at t=0, meaning that mathematically, expansion makes no sense and would not even be defined at the Big Bang.

The way to make the Big Bang understandable is to first slow down time near the Big Bang, since the universe initially expands extremely fast for t greater than zero. This is done by using a new time variable that is scaled to change much more slowly right after the Big Bang, when inflation is occurring. 

We'll label that new time variable N to distinguish it from the original time t. We also need to replace the Hubble variable with a new parameter that does not have an infinite value at the Big Bang, and instead will have a real numerical value there. That new value is called the "scaled Hubble variable" and it has a value of 0 at the Big Bang. The Big Bang makes sense in terms of the scaled Hubble variable and the new time, N.

To understand if our universe could have resulted from a previous one that crunched down, we need to see how the time values would change: If t is greater than 0, then we are in our universe, and if t is less than 0 then we would be in a previous universe. 

To mathematically justify a transition from one universe to another, we need to use a key parameter called the "Hubble scale factor" that measures how far, in distance, all the points of the universe are from one another. 

As you go back to the Big Bang, this distance approaches 0. This is seen by picking an arbitrary point in the universe, and from that point, the distance to each galaxy or any other location can be written as a relative distance, depending on the location, multiplied by a scale factor, "a" the Hubble scale factor.

As the universe expands or contracts uniformly in all directions, which we are assuming, then the single parameter a controls this. Therefore, a can be viewed as a uniform scale for the universe. This distance is 0 when t=0 since that is where the Big Bang starts. Right now, in our present space-time, astrophysicists give the Hubble scale factor a value of 1. 

Playing with the Hubble factor

Using regularization theory, I've been attempting to find if the Hubble factor can vary in a well-defined manner as t varies from less than 0 to greater than 0 — where a would approach 0 as the universe crunched down (for t less than 0, with t approaching 0), and where a=0 for t=0, and a would be greater than 0 after the Big Bang for t greater than 0. If that is the case, then this would be a mathematical way to justify the transition from the previous universe to ours. 

What does this mean in a more realistic, tangible sense? If you were in the contracting universe, it would appear much like our own universe, with its many galaxies, stars and other astronomical objects. As it contracted to the Big Bang — as the Hubble factor a approached 0 — all the objects would move closer and closer together, until they all coalesced into a singular state at a=0. The Big Bang would then occur and the new universe would start to rapidly expand. 13.75 billion years later, we would be where we are today. 

Of course, one would also have to argue that as time got sufficiently large, the universe would stop expanding and start to contract again in order to force the Hubble factor to go back to zero, starting another Big Bang and justifying that cyclic universes can occur over and over. 

That cyclic process is complicated by the existence of dark energy, which is causing the universe expansion to accelerate. A possible explanation for that acceleration might be due to the fact that a volume of space has an intrinsic energy to it, represented in astrophysics by a value called the cosmological constant. It isn't known if this acceleration slows down enough, perhaps due to the existence of dark matter, to contract. The nature of dark matter and energy is one of the great unknowns in cosmology, although together they account for 95.1 percent of the matter and energy of the universe.

Prime numbers and the Big Bang

In 2013, I published the first paper on using regularization to show that one universe can transition to another, having obtained an interesting and unexpected result. That study showed one universe can transition to another, provided the equation of state is equal to values that result from special prime number conditions. 

A prime number is a positive integer that is divisible only by one and itself, such as 1, 3, 5, 7, 11, 13 and so on. The conditions described in the paper specify certain pairs of integer numbers that are "relatively prime" — that is, there is no integer greater than 1 that divides them both. Relatively prime numbers need not be prime: For example, 7 and 8 are relatively prime and 8 is not a prime number. 

Remembering that the equation of state, labeled w, is the ratio of the pressure and density of the universe, then the density of the universe means basically the energy density, which is composed of the energy that is in the universe from matter and radiation. As the universe expands, density goes down since it needs to fill up a bigger space. The pressure value is a measure of a force acting on a given area, like a push. For example, radiation can cause such a pressure. When, for example, w is less than -1/3, this means that the universe has an accelerated expansion. The universe today has a w near -1 called the cosmological constant. When w is 0, that corresponds to a universe with only matter, while w=-1/3 corresponds to a universe with radiation and w=1 corresponds to a universe with anisotropy. 

Under the conditions described in the 2013 paper, w can only take values calculated from special relative prime numbers at or near the Big Bang, and that forces a huge restriction on w. Those conditions are based on integer numbers, since relatively prime numbers are integers, and are therefore very rare in the continuum of all numbers, where most numbers are actually not nice, clean integers, but irrational, like pi or the square root of 2. Integer numbers are also discrete — that is, groups of them don't form a smooth continuum. 

In the real world, such a condition may not make sense when one gets very close to the Big Bang. That is because when a is very near to 0 as the universe crunches down, a will get so small so that it is less than the Planck distance, where the laws of physics are no longer valid. 

In that region, the laws of quantum mechanics may dominate, yielding quantum fluctuations. These yield the variations of energy at a point in space due to Werner Heisenberg's uncertainty principle. If this occurs, then the relevance of the relative prime values of w may be lost, since the uncertainties of the energy would drown them out, something that modern theories would not be able to explain.

This result obtained in 2013 gave rise to "unique" transitions from one universe to another. As the universe crunched down and a approached 0 as t approached 0, when a=0 for t=0, there was only one unique transition, giving a unique universe for t greater than zero for each of these special discrete values of w. There could not be two or more transitions for each discrete w. Only one universe could result. This uniqueness could be lost due to quantum fluctuations near the Big Bang. This is because the uncertainties in the energy may not be able to distinguish between different relative prime number states for w.

That first paper modeled an idealized model of the universe where the equation of state was not allowed to vary as time varied. The other parameters were held fixed as well such as the anisotropy, curvature, etc., but in 2014, I worked with BingKan Xue of the Institute of Advanced Study in Princeton on a more realistic model. The equation of state as well as all the other parameters were allowed to vary as time varied. In this case, we restricted the equation of state to a value greater than 1, which, for technical reasons, implies that the energy component due to the variation of the equation of state dominates the contracting universe. The same results were obtained as in the previous results: The transitions, or extensions, of one universe to another are uniquely obtained for the same relatively prime conditions for w. I found this surprising since this model was far more complex than in the original paper. [The Cosmic Art of Edward Belbruno (Gallery )]

Alternate time

When w=1, it yields results that are much different than values that result when w is greater than 1. This is surprising in the following sense: Since w=1 can be reached from the case we had done for w greater than 1 as a limiting case, then as w gets closer and closer to 1, I expected w=1 to yield similar results as those for w greater than 1. That is, a unique transition from one universe to another, or no transition at all. It turns out that such a situation yields infinitely many different transitions, where each one is another universe. On the other hand, it wasn't surprising since BingKan and I could not study that case with the methods that were used for w greater than 1, since a certain key term in the Friedmann equations vanished. This term depended on the value of w and was not 0 when w was greater than 1. But when w=1, this term became 0 and then vanished from the equation. 

I realized that another mathematical methodology was needed, one that would result in non-unique extensions due to the vanishing of this term. This is because when this term was non-zero, for w greater than 1, a special mathematical theorem could be applied, called the stable manifold theorem. This yields unique extensions. When w=1 another mathematical theorem needs to be considered, called the center manifold theorem. This theorem yields non-unique extensions.

As a result, I found that the extension of a universe for t less than zero gave rise to infinitely many universes for t greater than zero. There seems to be no way to distinguish one from the other. The uniqueness was gone. 

However, of more interest, a new time variable was discovered at the Big Bang itself at t=0. I called the new variable, t-prime. At t=0, t-prime varies between plus and minus infinity. While t-prime is varying, then the Hubble factor, a and w are also varying. 

When t-prime starts from minus infinity, then w=-1 and a is plus infinity. This state corresponds to a universe that is infinitely large and where the equation of state corresponds to the cosmological constant representing pure expansion by dark energy. 

As t-prime approaches plus infinity, then a approaches 0, corresponding to where the universe has contracted to a singularity at the Big Bang, and w approaches 1, corresponding to a universe with anisotropy, or nonuniformity. Then when t-prime equals plus infinity, this corresponds to t=0 and a=0 and then the Big Bang occurs at w=1. While t-prime varies between plus and minus infinity, the Hubble variable has the value of plus infinity, meaning that the universe has infinite density, a strange state I call the extended Big Bang. 

It turns out that when the Big Bang occurs and t is greater than 0, then t-prime is also defined as well. This means that t-prime could be used as a time scale instead of the usual time, t. There is a mathematical relationship between these two time scales. At our epoch, they are essentially the same, but as one gets near to the Big Bang, they are much different. This new hidden time then becomes an alternate time.

The introduction of this time variable was done for mathematical purposes as described earlier, to find a slower time scale near the Big Bang. Its interpretation as being another time scale is convenient mathematically, but its physical relevance needs to be further studied. 

Art predicting the alternate time

As in other research where my art has predicted scientific discoveries with a new route to the moon and a theory regarding the origin of life on Earth, so has art inspired my work on alternate time.

After I finished the paper, I noticed an amazing connection of a painting I had done in 2009 that I had forgotten about. The painting is called Time, and it shows a scene consistent with the results of this paper. Two clocks represent two different time scales, while a circular object in the center, with lines emanating from an interior circle, can be viewed as representing the Big Bang. The little clock to the left connected to it can be viewed as the extended Big Bang time, t-prime. The big clock to the right can be viewed as our usual time, t. 

Unlike the other two cases I have written about, where the paintings were done simultaneously with the scientific work, this piece was done five years earlier. In fact, when I did it, it was totally unique to the style I was doing at the time. It was so different, I laid it aside, and didn't include it with my current focus. As a result, it received little exposure. 

I've now realized my unconscious mind was possibly working on this theory for all eight years, which was also suggested to me by Aggie Sung, a researcher in creativity in Princeton, New Jersey and who first pointed out to me the connection between my research with the painting Time. This painting actually predicted this result! This shows the power of the unconscious mind, which apparently does not abide by the same sense of time that we use. As I look at some of my new paintings, which are very abstract, I have to wonder if or what they are predicting in the world of science. 

Note: Meet Belbruno on Oct. 22 in New York at a Space.com gallery showing highlighting his work. Belbruno's art is available exclusively in the Space.com store.

Follow all of the Expert Voices issues and debates — and become part of the discussion — on Facebook, Twitter and Google+. The views expressed are those of the author and do not necessarily reflect the views of the publisher. This version of the article was originally published on Space.com.