Stephen Hawking: Everything you need to know about the thesis that 'broke the Internet'

Scribbled in pencil on one of its early pages is "no copying without the author's consent". In October 2017, Stephen Hawking allowed his PhD thesis — Properties of Expanding Universes — to be made available online through the University of Cambridge's Apollo portal. The website crashed almost immediately under the sheer weight of traffic. It was downloaded almost 60,000 times in the first 24 hours alone.

Hawking was 24 years old when he received his PhD in 1966 and, despite being diagnosed with motor neurone disease at just 21, could still handwrite that "this dissertation is my original work." In a statement to accompany its release, the late physicist said: "By making my PhD thesis Open Access, I hope to inspire people around the world to look up at the stars and not down at their feet; to wonder about our place in the universe and to try and make sense of the cosmos." 

Here, we break it down, guiding you through the physics until we reach the conclusion that made Hawking a household name.

Step 1: What’s it about?

Hawking's PhD thesis relates to Albert Einstein's General Theory of Relativity— the more accurate theory of gravity that replaced Isaac Newton's original ideas. Newton said gravity was a pull between two objects. Einstein said that gravity is the result of massive objects warping the fabric of space and time (space-time) around them. According to Einstein, Earth orbits the sun because we're caught in the depression our star makes in space-time.

Hawking applies the mathematics of general relativity to models of the birth of our universe (cosmologies). The earliest cosmologies had our universe as a static entity that had existed forever. This idea was so ingrained that when Einstein's original calculations suggested a static universe was unlikely, he added a "cosmological constant" to the math in order to keep the universe static. He would later reportedly call it his "greatest blunder".

Things began to change when Edwin Hubble made an important discovery. Hawking writes: "the discovery of the recession of the nebulae [galaxies] by Hubble led to the abandonment of static models in favor of ones in which we're expanding."

Step 2: Our expanding universe

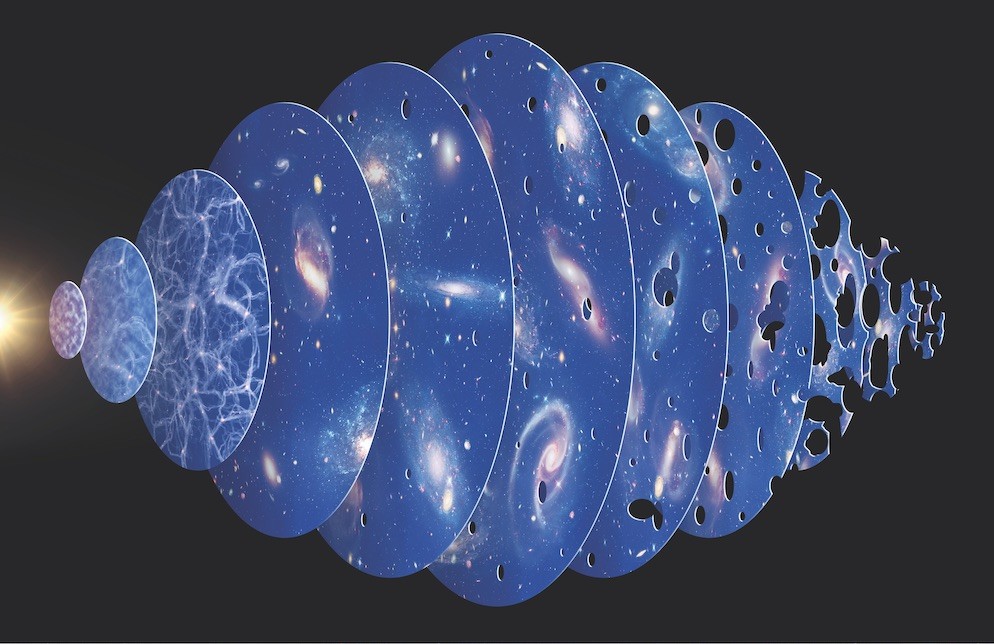
Some astronomers seized the idea of an expanding universe to argue that the universe must have had a beginning — a moment of creation called the Big Bang. The name was coined by Fred Hoyle, an advocate of the alternative Steady State Model. This theory states that the universe has been around forever, and that new stars form in the gaps created as the universe expands. There was no initial creation event.

Hawking spends chapter one of his thesis taking down the premise, formally encapsulated in a model called Hoyle-Narlikar theory. Hawking laments that although the General Theory of Relativity is powerful, it allows for many different solutions to its equations. That means many different models can be consistent with it. He says that's "one of the weaknesses of the Einstein theory."

The famous physicist then shows that a requirement of Hoyle-Narlikar theory appears to "exclude those models that seem to correspond to the actual universe." In short, the Steady State Model fails to match observation.

Step 3: Space: It looks the same everywhere

Hawking says that the assumptions of the Hoyle-Narlikar theory are in direct contradiction of the Robertson-Walker metric, named after American physicist Howard P. Robertson and British mathematician Arthur Walker. Today it is more widely called the Friedmann–Lemaître–Robertson–Walker (FLRW) metric. A metric is an exact solution to the equations of Einstein's General Theory of Relativity. Devised in the 1920s and 1930s, FLRW forms the basis of our modern model of the universe. Its key feature is that it assumes matter is evenly distributed in an expanding (or contracting) universe — a premise backed up by astronomical observations. 

Interestingly, Hawking offers Hoyle and Narlikar a ray of hope. "A possible way to save the Hoyle-Narlikar theory would be to allow masses of both positive and negative sign," he writes, before adding: "There does not seem to be any matter having these properties in our region of space." Today, we know that the expansion of the universe is accelerating, perhaps due to dark energy — a shadowy entity with an anti-gravitational property perhaps akin to particles with a negative mass.

Step 4: The problem with galaxies

Even geniuses get it wrong sometimes. Hawking's second chapter covers perturbations — small variations in the local curvature of space-time — and how they evolve as the universe expands. He says that a small perturbation “will not contract to form a galaxy." Later in the chapter he goes on to say: "We see that galaxies cannot form as the result of the growth of small perturbations."

That couldn't be further from our modern-day picture of how galaxies form. The key ingredient Hawking was missing is dark matter, an invisible substance thought to be spread throughout the universe, which provides a gravitational glue that holds galaxies together. Dark matter gathered around small space-time perturbations, eventually drawing in more and more material until early galaxies formed.

Our modern working cosmological picture is known as the ΛCDM model (pronounced Lambda CDM). Lambda is the Greek letter cosmologists use to denote the cosmological constant that Einstein originally introduced (albeit for the wrong reasons). CDM stands for cold dark matter. These two factors have been added to the FLRW model since Hawking wrote his thesis.

Step 5: Gravitational waves don’t disappear

Where Hawking was wrong on galaxies, he was very right on gravitational waves —ripples in the fabric of space-time that move outwards through the universe. They were predicted by Einstein when he first devised his Theory of General Relativity back in 1915, and in Hawking's time were also known as gravitational radiation.

Hawking uses Einstein's equations to show that gravitational waves aren't absorbed by matter in the universe as they travel through it, assuming the universe is largely made of dust. In fact, Hawking says that "gravitational radiation behaves in much the same way as other radiation fields [such as light]."

The physicist does note how esoteric the topic is in the 1960s. "This is slightly academic since gravitational radiation has not yet been detected, let alone investigated."

It would take physicists until September 2015 to detect gravitational waves for the first time using the Laser Interferometer Gravitational-Wave Observatory (LIGO). They were produced by the collision of two black holes — one 36- and the other 29-times the mass of the sun — about 1.3-billion-light-years away.

Related: Lab-grown black hole analog behaves just like Stephen Hawking said it would

Step 6: Are we living in an open, closed, or flat cosmos?

Hawking is heading for a groundbreaking conclusion, but first he sets himself up by introducing the idea of the overall shape of space. There are three general forms the curvature of space can take: open, closed, or flat.

A closed universe resembles Earth's surface — it has no boundary. You can keep traveling around the planet without coming to an edge. An open universe is shaped more like a saddle. A flat universe, as the name suggests, is like a sheet of paper. 

Imagine a triangle drawn onto the surface. We all learn at school that the angles inside a triangle sum to 180 degrees. However, that's only the case for triangles on flat surfaces, not open or closed ones. Draw a line from the Earth's North Pole down to the equator, before taking a 90-degree turn to travel along it. Then make another 90-degree turn back towards the North Pole. The angle between your path away from and towards the North Pole cannot be zero, so the angles inside that triangle must add up to more than 180 degrees.

Step 7: The universe is flat!

Hawking then links the idea of open and closed universes to Cauchy surfaces, named after the French mathematician and physicist Augustin-Louis Cauchy (1789—1857). A Cauchy surface is a slice through space-time, the equivalent of an instant of time. All points on the surface are connected in time. A path along a Cauchy surface cannot see you revisit a previous moment. In Hawking's own words: “A Cauchy surface will be taken to mean a complete, connected space-like surface that intersects every time-like and null line once and once only.”

He then says that closed universes are known as "compact" Cauchy surfaces, and open universes as “non-compact” ones. The former example is said to have "positive" curvature, the latter "negative" curvature. 

A flat universe has zero curvature. He moves on to set up the landmark assertions he's about to make about singularities by saying they are “applicable to models... with surfaces... which have negative or zero curvature.” Modern astronomers believe the universe is flat, meaning its zero curvature satisfies Hawking's conditions. 

Step 8: Hawking drops a bombshell

Most of the early chapters of Hawking's thesis are unremarkable — they don't offer anything particularly revolutionary, and he even gets a few things wrong. However, in his final chapter the physicist drops a bombshell that will make his name and ignite a stellar career, during which he will become one of the most famous scientists on the planet.

He says that space-time can begin and end at a singularity, and what's more he can prove it. A singularity is an infinitely small and infinitely dense point. It literally has zero size, and space and time both end (or begin) at a singularity. They had been predicted for decades, particularly when physicists started to apply Einstein's General Theory of Relativity to the picture of an expanding universe. 

If the universe is expanding today then it was smaller yesterday. Keep working back, and you find all matter in the universe condensed into a tiny, hot point — the moment of creation, a Big Bang. But just how do you prove that you can indeed get singularities in space-time?

Step 9: Hawking’s proof that the Big Bang happened

Hawking's proof leans on a very old method for proving a mathematical theory: Proof by contradiction. First you assume the thing you are trying to prove isn't true, then show that the resulting conclusions are demonstrably false. In fact, Hawking's most important section begins with the words "assume that space-time is singularity-free." There then follows some very complicated maths to show that such a universe would be simultaneously both open and closed — compact and non-compact at the same time. "This is a contradiction," Hawking said. "Thus the assumption that space-time is non-singular must be false." 

In one swoop, Hawking had proven that it is possible for space-time to begin as a singularity — that space and time in our universe could have had an origin. The Big Bang theory had just received a significant shot in the arm. Hawking started to write his PhD in October 1965, just 17 months after the discovery of the Cosmic Microwave Background— the leftover energy from the Big Bang. Together, these discoveries buried the Steady State Model for good.