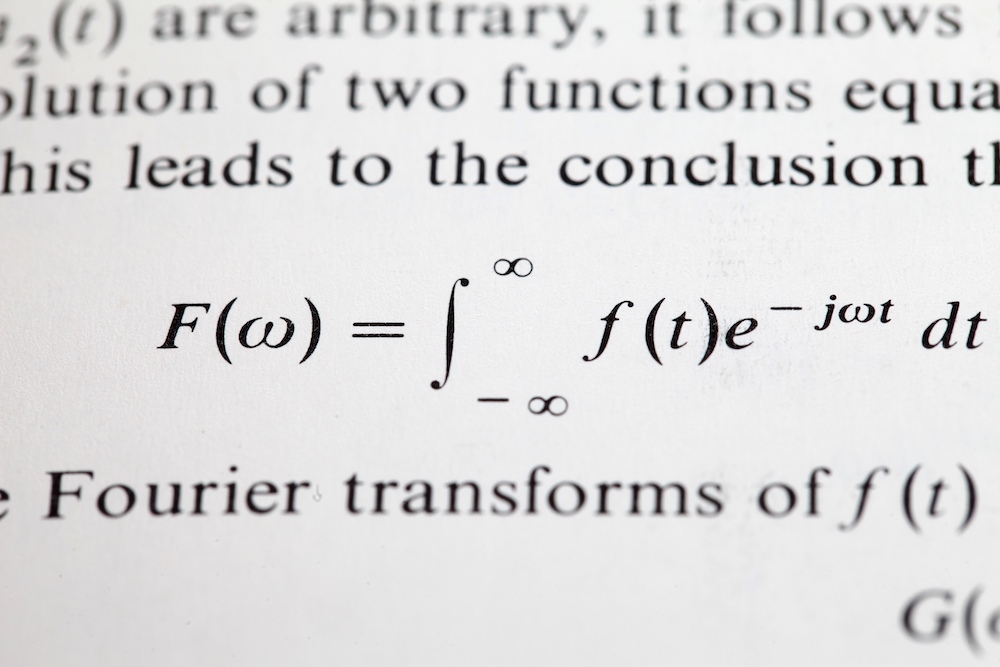
Breaking space news, the latest updates on rocket launches, skywatching events and more!
You are now subscribed
Your newsletter sign-up was successful
Want to add more newsletters?

Delivered daily
Daily Newsletter
Breaking space news, the latest updates on rocket launches, skywatching events and more!

Once a month
Watch This Space
Sign up to our monthly entertainment newsletter to keep up with all our coverage of the latest sci-fi and space movies, tv shows, games and books.

Once a week
Night Sky This Week
Discover this week's must-see night sky events, moon phases, and stunning astrophotos. Sign up for our skywatching newsletter and explore the universe with us!

Twice a month
Strange New Words
Space.com's Sci-Fi Reader's Club. Read a sci-fi short story every month and join a virtual community of fellow science fiction fans!
A mathematician who developed what some consider the "grand unified theory of mathematics" has won one of the most prestigious prizes in mathematics.
Robert Langlands, an emeritus professor at the Institute for Advanced Study at Princeton University, has won the Abel Prize, a prestigious mathematics prize that honors a lifetime of groundbreaking work, organizers of the prize announced yesterday (March 20).
Langlands, 81, won the prize for work in which he found deep connections between two seemingly disparate areas of mathematics: number theory and harmonic analysis, according to a statement from the organizers of the prize. [Images: The World's Most Beautiful Equations]
Early life
In his younger years, Langlands didn't seem destined for a life of the mind. Born in 1936 outside Vancouver, Canada, he grew up in a family that ran a building-supply store, and he wasn't particularly academic.
"School, except that it was a place frequented by girls and my friends, meant little to me," Langlands said in a 2010 interview with University of British Columbia graduate student Farzin Barekat. "I was probably the despair of the teachers, who, perhaps from the results of IQ tests, were aware that I had considerable untapped academic potential, from which I refused to profit."
He didn't even plan to go to a university until a teacher told him it would be a "betrayal of his God-given talents" if he didn't go, according to a biography of Langlands on the Abel Prize website.
But once he made it to college, his academic career took off. He earned a bachelor's degree and master's degree in mathematics from the University of British Columbia, and then a Ph.D. from Yale University. He then went on to become an instructor at Princeton University.
Breaking space news, the latest updates on rocket launches, skywatching events and more!
Breakthrough idea
It was at Princeton, on a school break, that the 30-year-old instructor had the insight that would shape the course of his mathematical life. When he returned to school, he mentioned his idea to the legendary mathematician André Weil when they bumped into each other in a hallway, and Weil told Langlands to write up his thoughts in a letter.
"If you are willing to read it as pure speculation, I would appreciate that," Langlands wrote to Weil. "If not — I am sure you have a wastebasket handy."
What followed was a 17-page letter that revealed secret connections between very different areas of mathematics.
In the letter, Langlands described a way to extend some of Carl Friedrich Gauss' pioneering work on prime numbers. Number theorists before Gauss had noticed a hidden relationship among primes: that all the primes that can be formulated as the sum of two squares (for instance, 2^2 + 1^2 = 5 or 3^2+2^2 = 13) have a remainder of 1 when divided by 4, but didn't know if it held true in all cases Quanta magazine reported. Gauss proved this idea in what's now known as the quadratic reciprocity law.
Langlands took Gauss' work and showed that the prime numbers that can be expressed as the sum of numbers raised to the third or fourth power (such as 1^3+2^3+4^3=73) can be tied to the distant mathematical realm of harmonic analysis. (This kind of analysis includes Fourier transforms, a mainstay tool used by scientists and engineers to analyze signals that have a periodic nature, such as sound waves or electromagnetic radiation spectra.)
Langlands showed that these two separate branches of mathematics can be directly related by using a special mathematical approach, a decoder ring of sorts, that became known as functoriality.
Langlands' work became so critical to math that his findings lured hundreds of other mathematicians into a new field of study that eventually became known as the Langlands program. And in 1995, when Andrew Wiles, a British mathematician, finally proved Fermat's last theorem, one of the most famous mathematical conjectures in history, he relied on Langlands' theory for a critical piece of the proof. (That theorem posits that there is no solution to the equation a^n+b^n=c^n for any n greater than 2 if a, b and c are all different numbers.)
Langlands will receive 6 million Norwegian krone (approximately $775,000) from Norway's King Harald V in a ceremony in Oslo, Norway, on May 22, according to the Abel Prize organizers.
Originally published on Live Science.

Tia is the assistant managing editor and was previously a senior writer for Live Science, a Space.com sister site. Her work has appeared in Scientific American, Wired.com and other outlets. She holds a master's degree in bioengineering from the University of Washington, a graduate certificate in science writing from UC Santa Cruz and a bachelor's degree in mechanical engineering from the University of Texas at Austin. Tia was part of a team at the Milwaukee Journal Sentinel that published the Empty Cradles series on preterm births, which won multiple awards, including the 2012 Casey Medal for Meritorious Journalism.

