What Is Parallax?
Parallax is the observed displacement of an object caused by the change of the observer's point of view. In astronomy, it is an irreplaceable tool for calculating distances of far away stars.
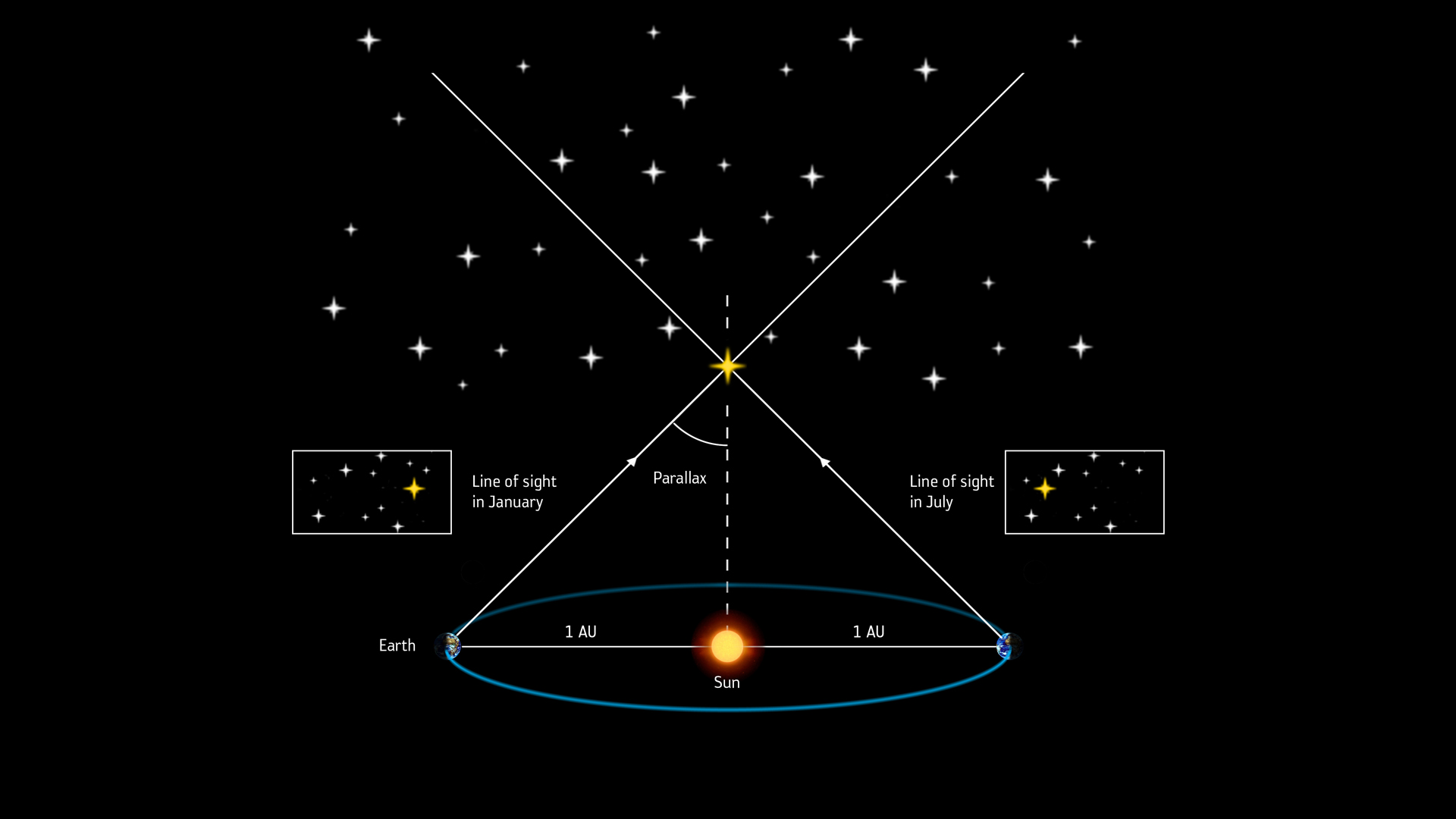
Observed from Earth, the night sky appears two-dimensional. But it's anything but. However, it took astronomers thousands of years to figure out how to measure distances of stars from our planet and create actual three-dimensional maps reflecting the distribution of stars and galaxies in the universe. One of the key methods they use is the so-called parallax, which relies on the same effect as stereoscopic vision.
It works like this: hold out your hand, close your right eye, and place your extended thumb over a distant object. Now, switch eyes, so that your left is closed and your right is open. Your thumb will appear to shift slightly against the background. By measuring this small change and knowing the distance between your eyes, you can calculate the distance to your thumb. That's trigonometry.
When it comes to measuring distances to other stars, there are no two eyes that could do the trick. Instead, the orbit of Earth around the sun provides the baseline for these calculations.
Every six months, the planet changes its position with respect to the surrounding universe by 186 million miles (300 million kilometers). Since we are making this motion together with Earth, we can (theoretically) observe its effect as tiny circles that stars perform in the sky every year. Due to the vast distances to even the nearest stars, these circles are barely noticeable so detecting and measuring them is extremely difficult.
Related: Milky Way galaxy: Facts about our galactic home
The history of parallax measurements in astronomy
The first known astronomical measurement using parallax didn't involve a star but the moon. The ancient Greek astronomer Hipparchus reportedly used observations of a solar eclipse from two different locations to calculate the distance of Earth's celestial companion.
In 1672, Italian astronomer Giovanni Cassini and his colleague Jean Richer made simultaneous observations of Mars, with Cassini in Paris and Richer in French Guiana. Cassini subsequently used those measurements to compute the parallax determining Mars' distance from Earth.
The first person to succeed at measuring the distance to a star using the parallax method was German astronomer Friedrich Bessel in 1838. Based on his observations, Bessel calculated that the star 61 Cygni, one of the stars in the Cygnus constellation, must be about 10 light-years away from Earth. This was the beginning of the long and tedious process of building a three-dimensional map of the universe.
In the late 1830s, Bessel’s contemporaries and rivals Wilhelm Struve and Thomas Henderson provided one parallax measurement each, bringing the total number to three. By the early 20th century, the list of stars with measured parallaxes grew to a few hundred, mostly thanks to the work of Dutch astronomer Jacobus Kapteyn.
Over the following decades, astronomers, aided by the improvements in telescope technology gradually grew the catalogs of stellar distances using the parallax method. In 1924, American astronomer Frank Schlesinger published a catalogue with the parallaxes of almost 2,000 stars, probing stellar distances out to a few dozen light-years from Earth. His catalogue was extended to about 6,000 stars by Louise Freeland Jenkins in 1952, and to over 8,000 stars by William van Altena in 1995. But the flickering effect caused by Earth's atmosphere and the distortion of the telescope observations caused by Earth's gravity prevented astronomers from reaching a precision better than about 0.01 arcseconds (one arcsecond is an angular measurement equal to 1/3600 of a degree).
"Today, with advanced technologies such as adaptive optics and interferometry, we can reach accuracies of a few dozen micro-arcsecond on large ground-based telescopes," Jos de Bruijne, an astronomer at the European Space Agency (ESA) said in a statement.

Breakthrough in parallax measurements and galaxy mapping
A real breakthrough in parallax measurement and therefore in determining distances of stars in our galaxy, the Milky Way, came with a mission called Hipparchos, after the ancient Greek astronomer that first used the method to estimate the distance of the moon.
This mission, launched by ESA in 1989, measured the positions and parallaxes as well as proper motions (the motion of a star on the sky observed over the years that is not caused by the parallax but reflects the actual movement of the star in space), for nearly 120,000 stars. The spacecraft orbited Earth for about four years, allowing astronomers to probe the neighbourhood of the sun up to the distance of 300 light-years with the accuracy of 0.001 arcseconds.
Two decades after the end of the Hipparchos mission, another breakthrough arrived. In 2013, ESA launched a telescope called Gaia that charts the positions, parallaxes, and proper motions of more than one billion stars. That number represents only about 1% of the actual number of stars in the galaxy, but that's enough for astronomers to extrapolate the observations to understand how the Milky Way behaves as a whole.
Using Gaia data, they could, for the first time, create a dynamic movie of the galaxy's life over billions of years, uncovering past events but also projecting what will happen in the future.
"Hipparcos had a detector with only one pixel and could only observe one star at a time," said de Bruijne, who is ESA's deputy project scientist for the Gaia mission. "Gaia, on the other hand, has nearly a billion pixels in its detectors and can observe thousands of stars at the same time."
Gaia’s mirrors are 20 times larger and therefore it collects light much more efficiently than its predecessor, seeing much deeper into the galaxy.
What else can you learn from the parallax?
The parallax method, however, is only the first rung on the cosmic distance ladder, a succession of methods that astronomers use to estimate distances of objects in the universe. At some point, stars and galaxies get too distant to have their parallax measured even by the most sensitive of available technologies. But astronomers can use insights derived from the parallax measurements of the closer stars to estimate distances of those more distant.
For example, by measuring the distances to a number of nearby stars, astronomers have been able to establish relationships between a star’s color and its intrinsic brightness, the brightness it would appear to have if viewed from a standard distance. These stars then become what astronomers call "standard candles." By comparing the color and spectrum of stars to the "standard candles", astronomers can determine the star's intrinsic brightness, said Mark Reid, an astronomer at the Harvard Smithsonian Center for Astrophysics.
By comparing the intrinsic brightness to the star's apparent brightness, we can get a good measure of the star's distance by applying the 1/r^2 rule. The 1/r^2 rule states that the apparent brightness of a light source is proportional to the square of its distance. For example, if you project a one-foot square image onto a screen, and then move the projector twice as far away, the new image will be 2 feet by 2 feet, or 4 square feet. The light is spread over an area four times larger, and it will be only one-fourth as bright as when the projector was half as far away. If you move the projector three times farther away, the light will cover 9 square feet and appear only one-ninth as bright.
If a star measured in this manner happens to be part of a distant cluster, we can assume that all of those stars are the same distance, and we can add them to the library of standard candles.
Using parallax for 3D Imaging
Another application of parallax is the reproduction and display of 3D images. The key is to capture 2D images of the subject from two slightly different angles, similar to the way human eyes do, and present them in such a way that each eye sees only one of the two images.
For example, a stereopticon, or stereoscope, which was a popular device in the 19th century, uses parallax to display photographs in 3D. Two pictures mounted next to each other are viewed through a set of lenses. Each picture is taken from a slightly different viewpoint that corresponds closely to the spacing of the eyes. The left picture represents what the left eye would see, and the right picture shows what the right eye would see. Through a special viewer, the pair of 2D pictures merge into a single 3D photograph. The modern View-Master toy uses the same principle.
Another method for capturing and viewing 3D images, Anaglyph 3D, separates images by photographing them through colored filters. The images are then viewed using special colored glasses. One lens is usually red and the other cyan (blue-green). This effect works for movies and printed images, but most or all of the color information from the original scene is lost.
Some movies achieve a 3D effect using polarized light. The two images are polarized in orthogonal directions, or at right angles to each other, typically in an X pattern, and projected together on the screen. The special 3D glasses worn by audience members block one of the two overlaid images to each eye.
Most of today’s 3D televisions use an active-shutter scheme to display images for each eye that alternate at 240 Hz. Special glasses are synchronized with the TV so they alternately block the left and right images to each eye.
Virtual reality gaming headsets, such as the Oculus Rift and the HTC Vive, produce 3D virtual environments by projecting an image from a different viewing angle to each eye to simulate a parallax effect.
There are also many uses for 3D imaging in science and medicine. For example, CT scans — which are actual 3D images of regions inside the body, not just a pair of 2D projections — can be displayed so each eye sees the image from a slightly different angle to produce a parallax effect. The image can then be rotated and tilted as it is being viewed. Scientists can also use 3D images to visualize molecules, viruses, crystals, thin film surfaces, nanostructures, and other objects that cannot be seen directly with optical microscopes because they are too small or are imbedded in opaque materials.
Additional resources and reading:
You can learn more about stellar parallax from Georgia State University's Department of Physics and Astronomy or watch a short lesson on the parallax angle from NASA. Once you master the basics, you can use the principles of parallax to create stereoscopic projects from MIT's Scratch Studios.
Bibliography
Parallax
https://sci.esa.int/web/gaia/-/60236-parallax (ESA, 2018)
Why was it so difficult to study the Milky Way before Gaia?
https://www.esa.int/Science_Exploration/Space_Science/Gaia/Why_was_it_so_difficult_to_study_the_Milky_Way_before_Gaia (ESA)
This article was updated on Dec. 12, 2018 by Space.com Contributor Adam Mann.
Join our Space Forums to keep talking space on the latest missions, night sky and more! And if you have a news tip, correction or comment, let us know at: community@space.com.
Breaking space news, the latest updates on rocket launches, skywatching events and more!

