The Universe Is Flat — Now What?

Breaking space news, the latest updates on rocket launches, skywatching events and more!
You are now subscribed
Your newsletter sign-up was successful
Want to add more newsletters?

Delivered daily
Daily Newsletter
Breaking space news, the latest updates on rocket launches, skywatching events and more!

Once a month
Watch This Space
Sign up to our monthly entertainment newsletter to keep up with all our coverage of the latest sci-fi and space movies, tv shows, games and books.

Once a week
Night Sky This Week
Discover this week's must-see night sky events, moon phases, and stunning astrophotos. Sign up for our skywatching newsletter and explore the universe with us!

Twice a month
Strange New Words
Space.com's Sci-Fi Reader's Club. Read a sci-fi short story every month and join a virtual community of fellow science fiction fans!
Paul Sutter is an astrophysicist at The Ohio State University and the chief scientist at COSI Science Center. Sutter is also host of Ask a Spaceman, RealSpace, and COSI Science Now.
Spoiler alert: The universe is flat. But there's a lot of subtlety packed into that innocent-looking statement. What does it mean for a 3D object to be "flat"? How do we measure the shape of the universe anyway? Since the universe is flat, is that…it? Is there anything else interesting to say?
Oh yes, there is.
Walk the line
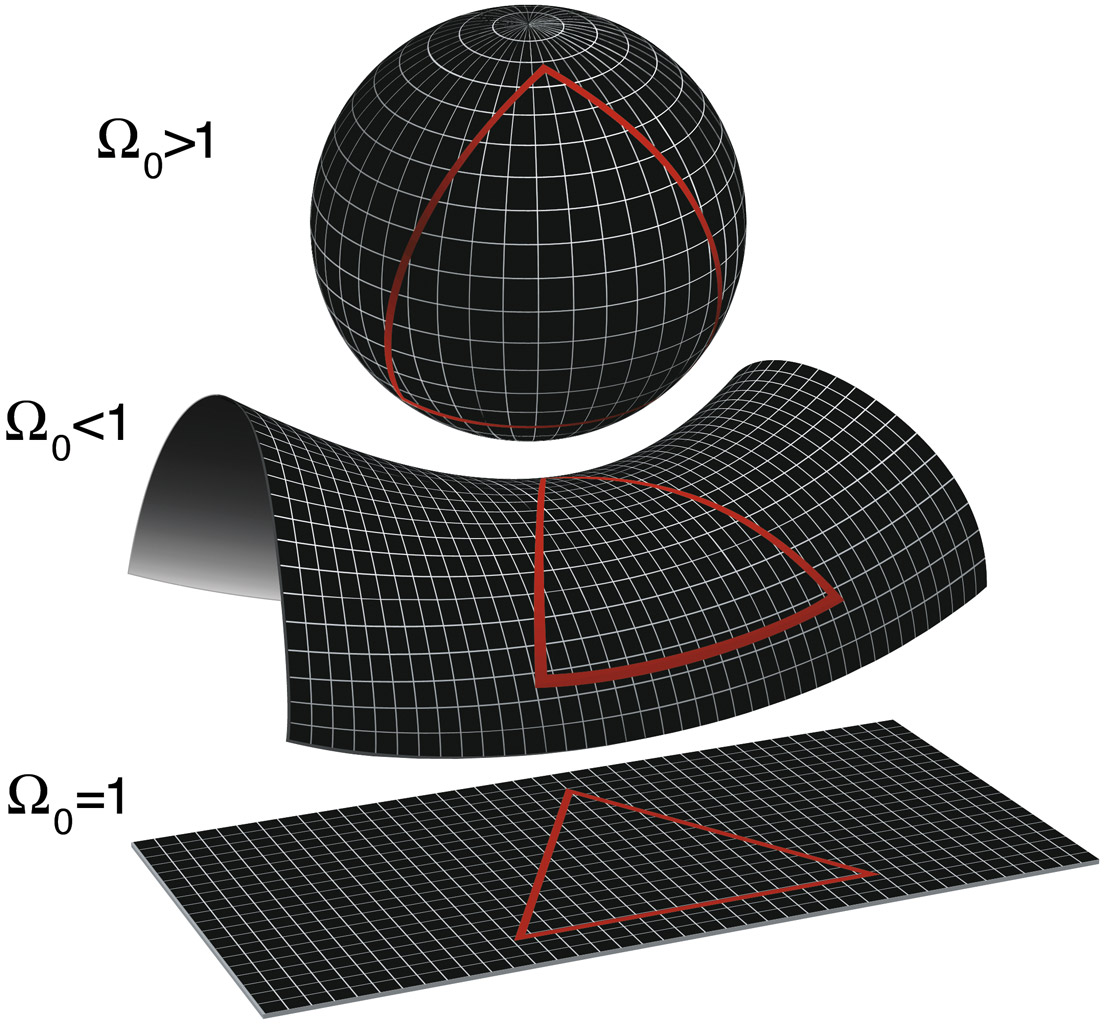
First, we need to define what we mean by flat. The screen you're reading this on is obviously flat (I hope), and you know that the Earth is curved (I hope). But how can we quantify that mathematically? Such an exercise might be useful if we want to go around measuring the shape of the whole entire universe. [The History & Structure of the Universe (Infographic)]
One answer lies in parallel lines. If you start drawing two parallel lines on your paper and let them continue on, they'll stay perfectly parallel forever (or at least until you run out of paper). That was essentially the definition of a parallel line for a couple thousand years, so we should be good.
Let's repeat the exercise on the surface of the Earth. Start at the equator and draw a couple parallel lines, each pointing directly north. As the lines continue, they never turn left or right but still end up intersecting at the North Pole. The curvature of the Earth itself caused these initially parallel lines to end up not-so-parallel. Ergo, the Earth is curved.
The opposite of the Earth's curved shape is a saddle: on that surface, lines that start out parallel end up spreading apart from each other (in swanky mathematical circles this is known as "ultraparallel"). [I explore the possible shapes of the universe in this video.]
Breaking space news, the latest updates on rocket launches, skywatching events and more!
So there you have it: You can measure the "flatness" of a structure just by watching how parallel lines behave. In our 3D universe, we could watch beams of light: If, say, two lasers started out perfectly parallel, then their long-term behavior would tell us important things.
Flat as a (big) pancake
Remember that measuring the shape of the universe is a question for cosmology, the study of the entire universe. And in cosmology, nobody cares about you. Or me. Or solar systems. Or black holes. Or galaxies. In cosmology we care about the universe only at the very largest scales; small-scale bumps and wiggles are not important for this question.
The universe has all sorts of deformations in space-time where it varies from the perfectly flat. Any place where there's mass or energy, there's a corresponding bending of space-time — that's General Relativity 101. So a couple light beams would naturally collide inside a wandering black hole, or bend along weird angles after encountering a galaxy or two.
But average all those small-scale effects out and look at the big picture. When we examine very old light — say, the cosmic microwave background — that has been traveling the universe for more than 13.8 billion years, we get a true sense of the universe's shape. And the answer, as far as we can tell, to within an incredibly small margin of uncertainty, is that the universe is flat.
There is no spoon
Well, that settles that. But this article isn't over yet, which means there's more to the story.
Have you ever asked yourself if there's a difference between a cylinder and a sphere? More than likely not, but it's never too late to try new things.
Take out your piece of paper with two parallel lines on it. Go ahead, dig it out of the trash. Wrap one end around to meet the other, making a cylinder. Carefully observe the parallel lines — they remain parallel, don't they? That's because cylinders are flat.
You heard it here first: Cylinders are flat.
There's an important distinction between geometry, the behavior of parallel lines, and topology, the way a space can get all twisted up. While the geometry of the universe is very well measured (again, it's flat), the topology is not. And here's a bonus fact: not only can we not determine the topology of the universe from observations, but there are also no laws of physics that predict or restrict the topology.
With your 2D piece of paper, you can connect the ends a few different ways. Connect one of the dimensions normally and you have a cylinder. Flip one edge over before connecting and you've made a Mobius strip. Connect two dimensions, the top to the bottom and one side to the other, and you have a torus (aka a donut).
In our 3D universe, there are lots of options — 18 known ones, to be precise. Mobius strips, Klein bottles and Hantzsche-Wendt space manifolds are all non-trivial topologies that share something in common: if you travel far enough in one direction, you come back to where you started. In the case of flipped dimensions, when you come back to your starting point, you'll find yourself upside down without having tried to do so at all. [Watch: Explaining the Shape of the Universe.]
Of course we've looked to see if our universe is connected like this; we don't see any copies of galaxies, and we don't see the cosmic microwave background intersecting itself. If the universe is pretzeled-up, it's on scales far, far larger than what we can observe.
So don't get too excited by possibility of living in a real-life version of the "Asteroids" game — which, as you now know, is played on the surface of a donut.
Learn more by listening to the episode "What's the shape of the universe?" on the Ask A Spaceman podcast, available on iTunes and on the Web at http://www.askaspaceman.com. Thanks to Greg S. and Michael W. for the questions that led to this piece! Ask your own question on Twitter using #AskASpaceman or by following Paul @PaulMattSutter and facebook.com/PaulMattSutter.
Follow us @Spacedotcom, Facebook and Google+. Original article on Space.com.

Paul M. Sutter is a cosmologist at Johns Hopkins University, host of Ask a Spaceman, and author of How to Die in Space.