Why do some James Webb Space Telescope images show warped and repeated galaxies?

News
By
published

The key to weird-looking and repeating galaxies is a phenomenon first predicted by Albert Einstein over 100 years ago.

Jump to:

This James Webb Space Telescope deep-field image shows some of the earliest and most distant galaxies ever seen. (Image credit: NASA, ESA, CSA and STScI)

In July 2022, the James Webb Space Telescope (JWST) — the most powerful telescope humanity has ever put into space — delivered its first photo, a deep-field image containing thousands of galaxies, many of which were seen as they were in the early universe. What many people didn't expect was how strangely warped and twisted some of these galaxies would appear. 

These Salvador Dalí-esque galaxies that look like melted taffy aren't representative of how these objects look in space; it's an illusion in the JWST images. Another startling aspect of the JWST images, such as the one taken of the massive galaxy cluster RX J2129, is that several galaxies appear at multiple points in the same image. Again, this is an illusion; these galaxies don't actually have exact doppelgängers. 

How is this possible? These two distinct aspects of JWST images are the result of the same phenomenon, called gravitational lensing. First predicted over 100 years ago by Albert Einstein, gravitational lensing has become an important tool for astronomers by acting as a "magnifying glass." These distorted and repeated galaxies are all examples of gravitationally lensed objects. 

Related: James Webb Space Telescope images: 12 astonishing views of our universe (gallery) 

What is gravitational lensing?

A gravitational lens magnifies the distant Cosmic Seahorse galaxy in this James Webb Space Telescope image released on March 28, 2023. (Image credit: ESA/Webb, NASA & CSA, J. Rigby)

Gravitational lensing is a phenomenon predicted by Einstein's theory of general relativity, which suggests that gravity emerges from the effect that objects with mass have on the fabric of space and time, united as a single entity called space-time.

Think of a stretched rubber sheet with balls of various masses placed on it. The more mass the ball has, the more it warps the rubber sheet. The same is true of objects with great mass sitting in the fabric of space-time: The greater the mass, the more an object warps space-time, with objects such as galaxies and galaxy clusters causing an extreme warping of space-time. This effect gets really interesting when light from a background object, like a star or a galaxy, passes this warp. 

Related: James Webb Space Telescope spots the Cosmic Seahorse through a gravitational lens (photo)

An illustration of two galaxies 'weighing down' the fabric of space-time. (Image credit: NASA/JPL-Caltech)

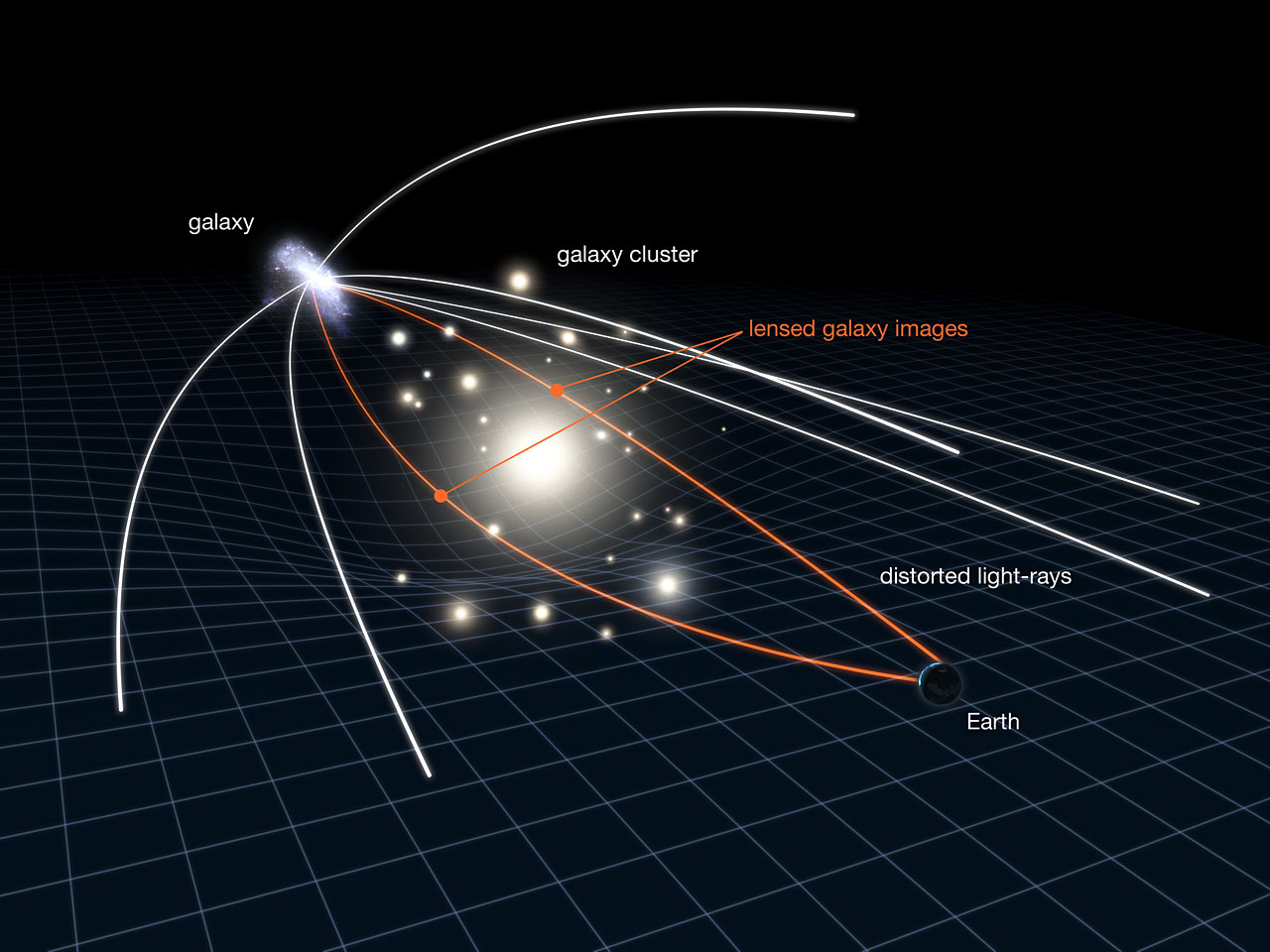
Light travels in straight lines, apart from when the space it is traveling through is warped. The warping of space by mass causes light from a distant source to "bend." As a result, when the light reaches Earth, it makes the background object appear to be in a different location in the sky.

In cases of extreme warping, when the object between Earth and the background source is massive, light takes different paths around the object, all of which are bent to varying degrees. This alters the length of the path the light takes to reach us to varying degrees and, thus, its arrival time. That means a lensed object can appear at multiple points in a single exposure. This can give rise to some interesting shapes, like crosses, or, in the case of lensing with perfect symmetry, a light ring called an "Einstein ring," all of which are made up of repeat occurrences of the same object. 

The graphic illustrates gravitational lensing in action.  (Image credit: NASA, ESA & L. Calçada)

Galaxy clusters have a "messy" shape, with the masses lacking a central distribution, so when they act as intermediate or lensing objects, the lensing is anything but perfect, according to the European Space Agency. This causes the background lensed object to appear distorted as arcs around the lensing galaxy cluster, as is seen in the JWST deep-field image.

These lensing objects are more than mere visual curiosities, however. Gravitational lensing can be useful to astronomers in a number of ways. 

Gravitational lensing doesn't just distort the light from a background object; it can actually amplify this light, thereby boosting the very faint light from extremely distant objects, like early galaxies. As a result, gravitational lensing is vital to the investigation of the early universe by the JWST. 

In addition, the patterns that lensing objects create as light passes them can reveal a lot about that object, NASA explains. For example, gravitational lensing can reveal how matter is distributed in galactic clusters and galaxies.

Follow us on Twitter @Spacedotcom or on Facebook. 

Additional resources

Explore gravitational lensing in more detail with these resources from NASA. The Fermi National Accelerator Laboratory has also produced a helpful gravitational lensing explainer video on their Fermilab YouTube channel.  

Bibliography

Kelly, P. (2023, February 28). Seeing triple. ESA/Webb, NASA & CSA. https://esawebb.org/images/potm2302a/

NASA. (2022, September 30). Gravitational lensing. HubbleSite.  https://hubblesite.org/contents/articles/gravitational-lensing#:~:text 

Join our Space Forums to keep talking space on the latest missions, night sky and more! And if you have a news tip, correction or comment, let us know at: community@space.com.

Robert Lea
Robert Lea
Senior Writer

Robert Lea is a science journalist in the U.K. whose articles have been published in Physics World, New Scientist, Astronomy Magazine, All About Space, Newsweek and ZME Science. He also writes about science communication for Elsevier and the European Journal of Physics. Rob holds a bachelor of science degree in physics and astronomy from the U.K.’s Open University. Follow him on Twitter @sciencef1rst.

1 Comment Comment from the forums
  • Pentcho Valev
    "The warping of space by mass causes light from a distant source to "bend"."

    Bending or deflection is a direct consequence of the fact that photons fall towards the source of gravity as predicted by Newton's theory - their speed INCREASES like the speed of ordinary projectiles. This is so obvious that many Einsteinians teach it explicitly (the brainwashed scientific community neither understands nor cares):

    "To see WHY A DEFLECTION OF LIGHT WOULD BE EXPECTED, consider Figure 2-17, which shows a beam of light entering an accelerating compartment. Successive positions of the compartment are shown at equal time intervals. Because the compartment is accelerating, the distance it moves in each time interval increases with time. The path of the beam of light, as observed from inside the compartment, is therefore a parabola. But according to the equivalence principle, there is no way to distinguish between an accelerating compartment and one with uniform velocity in a uniform gravitational field. We conclude, therefore, that A BEAM OF LIGHT WILL ACCELERATE IN A GRAVITATIONAL FIELD AS DO OBJECTS WITH REST MASS. For example, near the surface of Earth light will fall with acceleration 9.8 m/s^2." http://web.pdx.edu/~pmoeck/books/Tipler_Llewellyn.pdf

    James Hartle, Gravity: An Introduction to Einstein's General Relativity, p. 113: "If we accept the equivalence principle, we must also accept that light falls in a gravitational field with the same acceleration as material bodies." https://www.amazon.com/Gravity-Introduction-Einsteins-General-Relativity/dp/0805386629

    Einstein's general relativity preposterously predicts that the speed of falling photons DECREASES:

    "Einstein first discovered the gravitational time dilation in 1911, on the basis of his equivalence principle. From the time dilation, he immediately deduced the slow-down and deflection of light in a gravitational field. His 1911 result for the reduction of the speed of light was in error by a factor of 2, but he corrected this a few years later, in his theory of General Relativity." https://arxiv.org/ftp/arxiv/papers/1102/1102.2870.pdf

    "Thus, as φ becomes increasingly negative (i.e., as the magnitude of the potential increases), the radial "speed of light" c_r defined in terms of the Schwarzschild parameters t and r is reduced to less than the nominal value of c." https://www.mathpages.com/rr/s6-01/6-01.htm
    Reply